ned Productions - nedtries

Computer science theory classes teach students that associative containers (i.e. containers whose items are placed in some form of faster than O(n) access index) come in two main forms: (i) ordered, in which case it has O(log N) average lookup complexity and (ii) unordered, in which case it has O(1) average lookup complexity. The C++ Standard Template Library comes with std::map<> and std::unordered_map<> for precisely this reason - there is supposedly no other choice except for esoteric requirements such as indexing a few terabytes of data where, as Wikipedia will show you, you'll find all sorts of crazy indexation algorithms.

So what if I told you that for the very common case of a pointer sized key lookup that the standard assumptions are wrong? What if there was an algorithm which provides one of the big advantages of ordered indexation which is close fit finds, except it has nearly O(1) complexity rather than O(log N) and is therefore 100% faster? What if, in fact, this algorithm is a good 20% faster than the typical O(1) hash table implementation for medium sized collections and is no slower even at 10,000 items?

You don't believe me? Well I didn't believe me either when I was developing the user mode page allocator for my memory allocator, nedmalloc. But seeing is believing, so here's some scaling graphs for a 2.67Ghz x64 Intel Core 2 Quad:

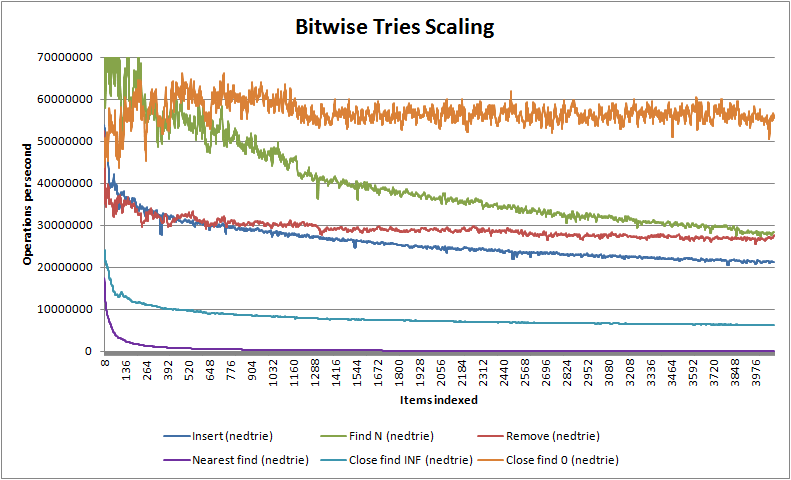
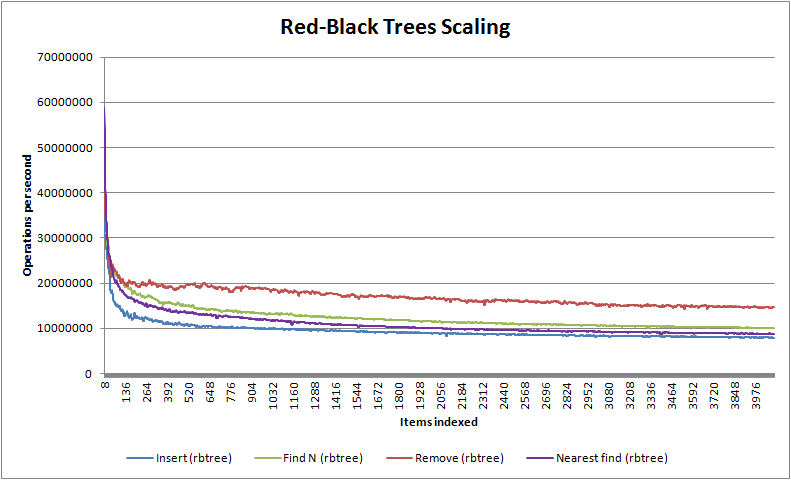
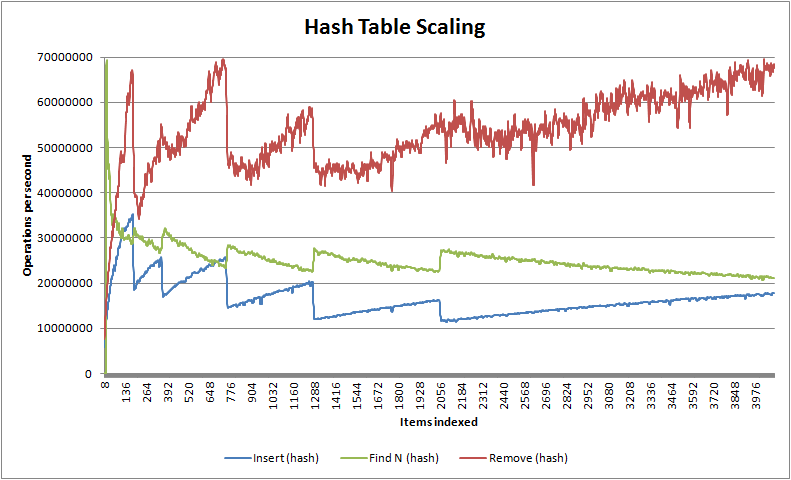
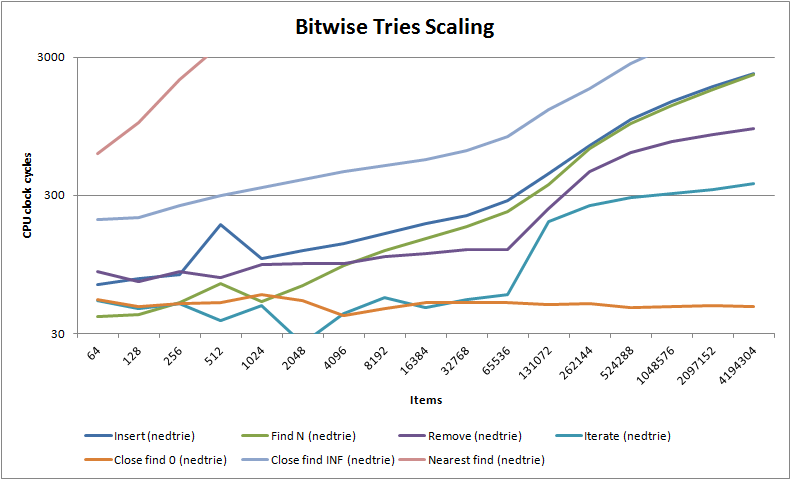
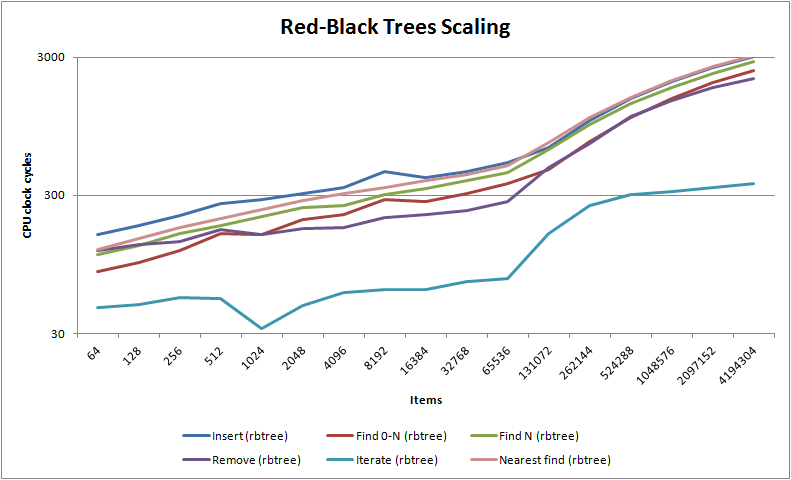
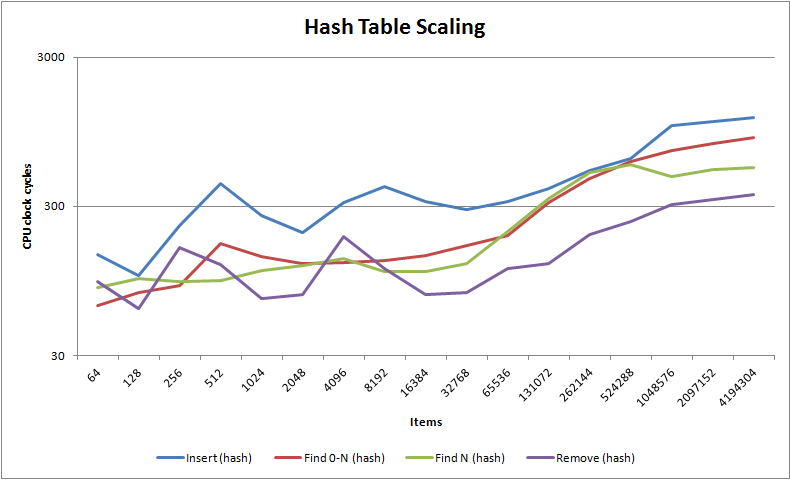
As you can see, nedtries utterly destroys the traditional red-black binary tree algorithm except for nearest fit finds where it has similar complexity - in fact, unless you have items whose difference cannot be converted into a stable size_t value (which is rare) then for most use cases you should probably never use red-black trees ever again, despite that they are the canonical algorithm for anything which needs to maintain how items relate to one another. You will also notice that for less than 64k items nedtries handily beats the venerable O(1) hash table where it is considerably faster at insertion and finding - only in deletion does the hash table shine. Note that unlike hash tables but like red-black trees, nedtries makes no use of dynamic memory unless you use the STL container emulations trie_map<> and trie_multimap<>.

You will also note the most interesting characteristic of bitwise tries of all: insertion, deletion and finds (including close fit finds) all take about the same amount of time. Almost every other search algorithm will be good at one or two things but bad at the others e.g. hash tables are fast at searching and deletion but slow at inserting. If your code, like a lot of common code, equally does inserts and deletes as it does finds then nedtries will do wonders for your software project.

How does it work?

It works by constructing a binary tree based on individual bit difference, so the higher the entropy (disorder) between key bits, the faster nedtries is relative to other algorithms (equally, the more similar the keys at bit level the slower it goes). It hence has a complexity for a given key of O(1/D_KL(key||average key)) which is the inverse of the Kullback–Leibler divergence (i.e. relative entropy) between the entropy of the key you are searching for and the average entropy of the key in the tree. Its worst case complexity - where all keys are almost identical - is O(log₂ N). This implies that for well distributed keys that average complexity will always be a lot better than red-black trees, but somewhat worse than O(1) because for obvious reasons, more keys means more unique information and therefore there is always some scaling relation to the number of keys in the tree i.e. the Kolmogorov complexity, or the compressed length, of all keys.

If that hurt your head, it's actually very easy to understand: make sure your keys are well distributed and nedtries will fly, but it isn't quite pure O(1) like a hash table. As you can see in the scaling graphs above, it's much more sensitive to your L2 cache size than a hash table, so once you exceed that number of items a hash table will always win. Therefore, in practice nedtries ought to be used instead of a hash table only up to about 10,000 items after which a hash table is better, though hash tables do require additional dynamic memory allocation for their buckets while nedtries requires no dynamic memory at all. nedtries performs much better in every situation than red-black trees (as RB trees write out a lot of memory as they rebalance themselves, invalidating caches across a SMP config which also makes them particularly ill suited for multiple thread use) except for one case: if you need guaranteed nearest match finds, red-black trees are unbeatable.

I hold that almost always where you're currently using a red-black tree or something very similar, you'll benefit if you replace that with nedtries, and where you're using a hash table with less than 10,000 items you probably will benefit from nedtries. If you can't use dynamic memory, nedtries is a no-brainer.

What implementations are there?

There is a C macro based implementation, a C++ template-through-the-C-macros implementation (this makes debugging vastly easier and lets the C++ compiler optimiser perform better) and two C++ STL API compatible containers which can be slotted in to replace any existing usage of std::map<>, std::unordered_map<>, std::multimap<> or std::unordered_multimap<> (or any of their very similar kin).

The code is 100% C and C++ standard code. If you have a C++11 supporting compiler it will make use of any move constructors you might have.

If you don't understand the algorithm and decide you need to, I'd suggest compiling it as C++ and stepping through it using a debugger.

In more recent years there are competing implementations of bitwise tries. TommyDS contains one, also an in-place implementation, which appears to perform well. Note that the benchmarks he has there compare the C version of nedtries which is about 5-15% slower than the C++-through-the-C-macros version, and I am also unsure if he told the compiler it can use the conditional instructions (CMOV) available since the Pentium Pro as he is compiling nedtries for 32-bit x86. CMOV makes a big difference to nedtries' performance.

Where do I get it from?

You can download a source zip from github or from sourceforge. The current stable version is v1.02 final (9th July 2012). The latest trunk version is v1.03 trunk.

You can also pull a full GIT clone from either of:

API reference documentation can be found here.

How do I report bugs, suggest enhancements or get support?

Please report bugs or enhancements to the github issue tracker. You can get non-commercial support from the email address at the bottom of this page, or you can get commercial support from my company ned Productions Consulting Ltd.

Changelog:

v1.03 trunk (?):

Added some support for architectures where CHAR_BIT is not 8. Thanks to Sebastian Ramadan for contributing this.
Disable the STL container being compiled by default, and stop suppressing warnings about strict aliasing type punning.

v1.02 Final (9th July 2012):

Due to the breaking change in what NEDTRIE_NFIND means and does, bumped version number.
[master 910ef60] Fixed the C++ implementation causing memory corruption when built as 64 bit.
[master 0ea1327] Added some compile time checks to ensure C++ implementation will never again cause memory corruption when built as 64 bit.

v1.01 RC2 (unreleased):

[master bd6f3e5] Fixed misc documentation errors.
[master 79efb3a] Fixed really obvious documentation bug in the example usage. Thanks to Fabian Holler for reporting this.
[master 99e67e3] Fixed that the example usage in the documentation spews warnings on GCC. Now compiles totally cleanly. Thanks to Fabian Holler for reporting this.
[master 537c27b] Added NEDTRIE_FOREACH_SAFE and NEDTRIE_FOREACH_REVERSE_SAFE. Thanks to Stephen Hemminger for contributing this.
[master 4b12a3c] Fixed the fact that I had forgotten to implement iterators for trie_map<>. Also added trie_multimap<>. Thanks to Ned for pointing out the problem.
[master 8b53224] Renamed Nfind to Cfind.

v1.01 RC1 (19th June 2011):

[master 30a440a] Fixed misc documentation errors.
[master 2103969] Fixed misoperation when trie key is zero. Thanks to Andrea for reporting this.
[master 083d94b] Added support for MSVC's as old as 7.1.
[master f836319] Added Microsoft CLR target support.
[master 85abf67] I, being a muppet of the highest order, was actually benchmarking the speed of the timing routines rather than much else. Performance is now approx. 10x higher in the graphs ... I am a fool!
[master 6aa344e] Added check for key uniqueness in benchmark test (hash tables suffer is key isn't unique). Added cube root averaging to results output.
[master feb4f56] Replaced the use of rand() with the Mersenne Twister ( http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/SFMT/index.html).

v1.00 beta 1 (18th June 2010):

[master e4d1245] First release.

ned Productions – nedtries